作者简介: 一位热爱科学研究的Matlab仿真开发人员。他在修炼心智的同时,也提升了自己的技术。 matlab项目合作请私信。
个人主页:Matlab研究工作室
个人信条:调查事物以获得知识。
点击查看更完整的Matlab代码和仿真定制内容
智能优化算法神经网络预测雷达通信无线传感器电力系统
信号处理图像处理路径规划元胞自动机无人机
球体同形曲面的准各向同性采样是计算机图形学和计算机视觉领域的一个重要问题。问题涉及如何在球体表面均匀采样点,以便更好地模拟现实世界的球形物体。
球体同胚表面准各向同性采样的挑战在于球体表面不是平面,而是曲面。因此,在球体表面均匀采样并不像在平面上那么简单。另外,球面的几何特性要求采样过程中需要考虑球面的曲率和各向异性。
为了解决这个问题,研究人员提出了许多不同的算法和技术。常用的方法之一是基于分形理论的采样方法。该方法利用分形几何的特性,通过迭代细分球体表面来实现均匀采样。该方法的优点是可以生成高质量的采样点,但缺点是计算复杂度较高。
另一种常见的方法是基于坐标变换的采样方法。该方法的工作原理是将球体表面上的点映射到更简单的坐标空间(例如二维平面或球面坐标系),然后在该空间中均匀采样。然后通过逆变换将采样点映射回球体表面。该方法的优点是简单、高效,缺点是可能引入一定程度的采样偏差。
除了这些方法之外,还有许多其他方法可用于球体同胚面的准各向同性采样。这些方法包括基于随机化的抽样方法、基于优化的抽样方法和基于统计的抽样方法。每种方法都有其优点和缺点,选择合适的方法取决于具体的应用需求和性能要求。
总而言之,球体同形曲面的准各向同性采样是一个具有挑战性的问题,但在计算机图形和计算机视觉中具有广泛的应用。通过研究和开发各种采样方法,可以更好地模拟和渲染球形物体,从而提高计算机图形学和计算机视觉的应用效果。
%% sphere_homeo_sfc_isotropic_splg
%
% 对给定球体同胚表面进行各向同性采样的函数。
%
% 作者支持: nicolas.douillet (at) free.fr,2017-2020。
%
句法
%
% sphere_homeo_sfc_isotropic_splg(fctn_x, fctn_y, fctn_z);
%
% sphere_homeo_sfc_isotropic_splg(fctn_x, fctn_y, fctn_z, range_u, range_v);
%
% sphere_homeo_sfc_isotropic_splg(fctn_x, fctn_y, fctn_z, range_u, range_v, option_random_sampling);
%
描述
%
% sphere_homeo_sfc_isotropic_splg(fctn_x, fctn_y, fctn_z)
% 生成X、Y、Z坐标的三分号向量/[60*120 3]矩阵
采样球同胚表面的点的百分比定义为
% 函数处理fctn_x、fctn_y 和fctn_z。
%
% sphere_homeo_sfc_isotropic_splg(fctn_x, fctn_y, fctn_z, range_u, range_v)
% 生成位于该区域的range_u(1,3)*range_v(1,3)个样本
% [min(u), max(u)] x [min(v) max(v)]=[range_u(1,1), range_u(1,2)] x [range_v(1,1) range_v(1 ,2)]
%
% sphere_homeo_sfc_isotropic_splg(fctn_x, fctn_y, fctn_z, range_u, range_v, option_random_sampling)
% 如果option_random_sampling=1,则随机采样,
% else -option_random_sampling=0 - 采样是均匀的。
%
也可以看看
%
% https://fr.mathworks.com/matlabcentral/fileexchange/64307-torus-homeomorphic-surface-quasi-isotropic-sampling?s_tid=prof_contriblnk torus_homeo_sfc_isotropic_splg|
% https://fr.mathworks.com/matlabcentral/fileexchange/69212-geoid 大地水准面|
% https://fr.mathworks.com/help/matlab/ref/rand.html 兰特|
% https://fr.mathworks.com/help/matlab/ref/mesh.html 网格|
% https://fr.mathworks.com/help/matlab/ref/trimesh.html 修剪网格
%
%%输入参数
%
% - fctn_x : x 方向的函数句柄,在球坐标中,假设向量和矩阵重载。
%
% - fctn_y : y 方向的函数句柄,在球坐标中,假设向量和矩阵重载。
%
% - fctn_z : z 方向的函数句柄,在球坐标中,假设向量和矩阵重载。
%
% - range_u : 双实数行向量,u 类型的参数向量: [min(u), max(u), nb_samples_u]。
%
% - range_v : 实数行向量double,v 类型的参数向量: [min(v), max(v), nb_samples_v]。
%
% - option_random_sampling : 逻辑,*true (1) /false (0)。
%
%%输出参数
%
% [| | |]
% - M=[X Y Z],实数矩阵双精度,点集。大小(M)=[nb_samples_u * nb_samples_v 3]。
% [| | |]
%
% - u : double实矩阵,u方向的采样矩阵/网格。大小(u)=[nb_samples_u,nb_samples_v]。
%
% - v : double实矩阵,v方向的采样矩阵/网格。大小(v)=[nb_samples_u,nb_samples_v]。
%
% [ | | | ]
% - T=[i1 i2 i3],正整数矩阵double,三角剖分。大小(T)=[nb_triangles,3]。
% [ | | | ]
%
% 其中nb_triangles=nb_samples_u*(nb_samples_v-2)。
% T 仅在option_random_sampling=false/0 的情况下相关。
%
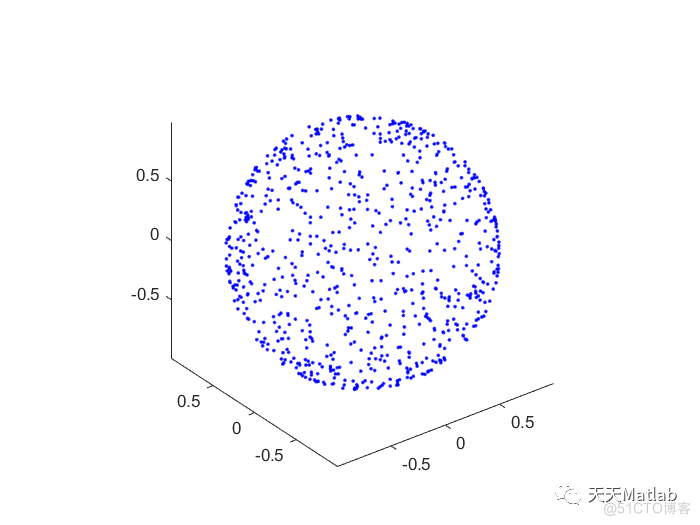
%% 示例#1
% 各向同性随机抽样
fctn_x=@(u,v)sin(u).*cos(v);
fctn_y=@(u,v)sin(u).*sin(v);
fctn_z=@(u,v)cos(u);
范围_u=[0 pi 20]; % 球体的纬度角
range_v=[0 2*pi 40]; % 球体的经度角
[M1, u1, v1]=sphere_homeo_sfc_isotropic_splg(fctn_x, fctn_y, fctn_z, range_u, range_v);
数字;
plot3(M1(:1), M1(:2), M1(:3), 'b.'), 等等;
轴相等、轴方、轴紧;
颜色图([0 0 1]);
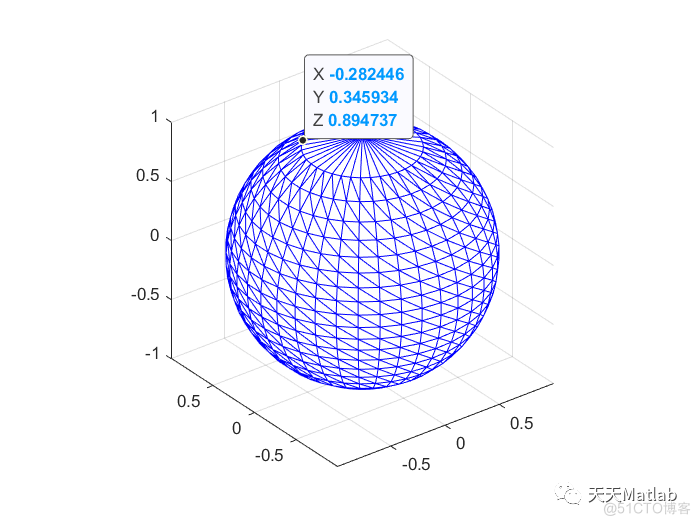
%%示例#2
% 各向同性定期采样
[M2, u2, v2, T]=sphere_homeo_sfc_isotropic_splg(fctn_x, fctn_y, fctn_z, range_u, range_v, 0);
TRI=三角测量(T, M2(:1), M2(:2), M2(:3));
数字;
修剪网格(TRI),坚持;
轴相等、轴方、轴紧;
颜色图([0 0 1]);
010- 1010
010- 1010